Step-by-step explanation
The slope of a line is a measure of its steepness. Mathematically, the slope is calculated as "rise over run" (change in y divided by change in x).
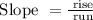
Since the slope of the line segment AB is 3/4, we know that its rise is 3, and its run is 4.
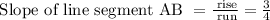
So, the coordinates of points A and B could be A(0,0) and B(4,3).
On the other hand, the rule for a rotation by 180° about the origin is:
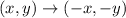
Then we can apply the above rule and calculate the coordinates of line segment A'B'.
![\begin{gathered} A(0,0)\operatorname{\rightarrow}A^(\prime)(0,0) \\ B(4,3)\operatorname{\rightarrow}B^(\prime)(-4,-3) \end{gathered}]()
Finally, let us find the slope of the line segment A'B'.
As we can see, the slope of the line segment A'B' is also 3/4.
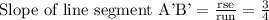
Answer
Supports Jessie's claim