Part A)
The power (P) delivered by an electric current (I) passing through a voltage (V) is given by the equation:
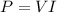
The power P and the voltage V are given, and the current I is unknown. Isolate I from the equation and replace P=1kW and V=120V to find the magnitude of the current that the portable heater will draw:
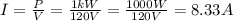
Therefore, the portable heater will draw 8.33 Amperes.
Part B)
The electric current (I) is the rate of transfer of electric charge (Q) per unit time (t):
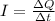
On the other hand, a current of one Ampere transfers a Coulomb of charge in one second. Isolate ΔQ from the equation, replace I=8.33A and Δt=1.0min=60s to find the charge delivered in 1.0 minute:
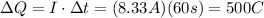
Therefore, 500 Coulomb of charge will be delivered to the portable heater in 1.0 minute.
Part C)
Let N be the number of electrons transferred to the heater. If e is the charge of a single electron, and a total charge of 500 Coulomb is transferred to the heater, then:
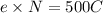
Isolate N from the equation:
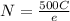
Replace the value of the charge of a single electron to find the number of electrons:
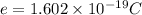
Then:
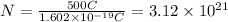
Then, 3.12*10^21 electrons are transferred.
Part D)
Since power is the rate of transfer of energy with respect to time, then:
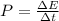
Isolate ΔE and replace P = 1kW and Δt = 60s to find the total energy delivered to the heater:
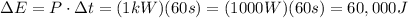
Therefore, the energy delivered to the heater is 60,000 Joules.
Part E)
The resistance of a circuit is defined as the quotient between the voltage of the circuit and the current that passes through it:
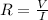
Replace V=120V and I=8.33A to find the resistance of the heater:
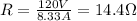
Therefore, the resistance of the heater is 14.4 Ohm.
Part F)
Assuming that the resistance of the heater does not change, we can isolate I from the definition of resistance and replace V=220V to find the current tha would pass through the heater if plugged into a 220V circuit:
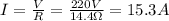
Since 15.3 A is more than 10A, then, the heater will burn out.