To solve the exercise you can use the point-slope formula, that is,

So, in this case, you have

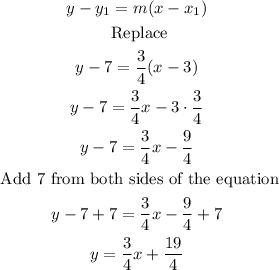
Therefore, the equation of the line is
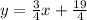
Finally, to find the x-coordinate of point A, replace y = 5 into the equation of the line you just found and solve for x

Therefore, if point A(x,5) lies on the line, the value of x is 1/3.