Question

Construct two prisms that are proportional and provide the dimensions of your prism and calculate the surface area and volume of each prism .

Answer 1

Let A and B be two rectangular prisms which are proportional.

The dimensions of rectangular prism A:

Length, l=10 cm.

Width, w=5 cm.

Height, h=3 cm.

The dimensions of rectangular prism B:

Length, L=20 cm.

Width, w=10 cm.

Height, h=6 cm.

Two prisms are proportional if the ratio of the corresponding dimensions of the prisms are equal.

The ratio of corresponding dimensions of prism A to B is,

`\begin{gathered} (l)/(L)=\frac{10\text{ cm}}{20\text{ cm}}=(1)/(2) \\ (w)/(W)=\frac{5\text{ cm}}{10\text{ cm}}=(1)/(2) \\ (h)/(H)=\frac{3\text{ cm}}{6\text{ cm}}=(1)/(2) \end{gathered}`

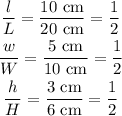
Since the ratios of lengths, widths and heights are equal, the prisms A and B are proportional.

Now, the volume of rectangular prism A is,

`\begin{gathered} V_A=\text{lwh} \\ =10*5*3 \\ =150cm^3_(\rbrack) \end{gathered}`

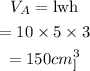
The surface area of rectangular prism A is,

`\begin{gathered} S_A=2(lw+lh+wh) \\ =2(10*5+10*3+5*3) \\ =2(50+30+15) \\ =2*95 \\ =190cm^2 \end{gathered}`

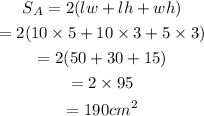
Therefore, the volume of rectangular prism A is 150 cu.cm and the surface area rectangular prism A is 190 sq.cm.

The volume of prism B is,

`\begin{gathered} V_B=LWH \\ =20*10*6 \\ =1200cm^3 \end{gathered}`

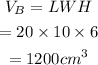
The surface area of prism B is,

`\begin{gathered} S_B=2(LW+LH+WH) \\ =2(20*10+20*6+10*6) \\ =2(200+120+60) \\ =2*380 \\ =760cm^2 \end{gathered}`

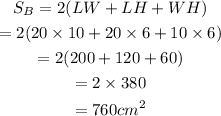
Therefore, the volume of rectangular prism A is 1200 cu.cm and the surface area rectangular prism A is 760 sq.cm.

A rought sketch of the prism is shown below: