Let A and B be two rectangular prisms which are proportional.
The dimensions of rectangular prism A:
Length, l=10 cm.
Width, w=5 cm.
Height, h=3 cm.
The dimensions of rectangular prism B:
Length, L=20 cm.
Width, w=10 cm.
Height, h=6 cm.
Two prisms are proportional if the ratio of the corresponding dimensions of the prisms are equal.
The ratio of corresponding dimensions of prism A to B is,
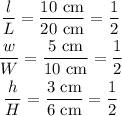
Since the ratios of lengths, widths and heights are equal, the prisms A and B are proportional.
Now, the volume of rectangular prism A is,
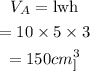
The surface area of rectangular prism A is,
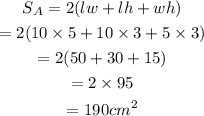
Therefore, the volume of rectangular prism A is 150 cu.cm and the surface area rectangular prism A is 190 sq.cm.
The volume of prism B is,
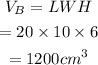
The surface area of prism B is,

Therefore, the volume of rectangular prism A is 1200 cu.cm and the surface area rectangular prism A is 760 sq.cm.
A rought sketch of the prism is shown below: