Question

which of the following statements must be true about this diagram? check all that apply. answers are with the picture below:

Answer 1

The external angle theorem states that the measure of the external angle of a triangle is equal to the sum of the two opposite internal angles.

In this case

`\angle4=\angle1+\angle2`

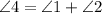
Then

∠4 is greater than ∠2 and ∠1, so A and B check

And F also checks

We know that the sum of the internal angles of a triangle add up to 180º so that:

`\angle1+\angle2+\angle3=180º`

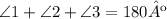
And we also know that ∠3 and ∠4 are a linear pair, this means that they also add up to 180º:

`\angle3+\angle4=180º`

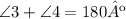
Since both expressions are equal to 180º we can conclude that they are equal:

`\angle1+\angle2+\angle3=\angle3+\angle4`

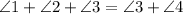
Subtract ∠3 from both sides of the equation and we get that

`\angle1+\angle2=\angle4`

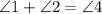
As stated by the external angle theore, the measure of the external angle, ∠4, of a triangle is equal to the sum of the opposite interior angles, ∠1+∠2 → With this, is proven that F is correct

If angles 1 and 2 add up to angle 4, then, by logic, their measure has to be less than angle 4

→ and this is how you know that ∠1 and ∠2 are less than ∠4