Given that:
- The manufacturing process produces on average 3% defective items.
- The company ships 15 items in each box.
- It wishes to guarantee no more than 1 defective item per box.
You need to use the following Binomial Distribution Formula in order to find the probability that the box will fail to satisfy the guarantee:
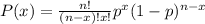
Where "n" is the number of trials, "x" is the number of successes desired, and "p" is the probability of getting a success in one trial.
In this case:
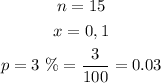
Since It wishes to guarantee no more than 1 defective item per box, you can set up that:
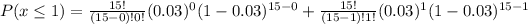
![undefined]()