Step 1: Find the standard error (SE)
The standard error is given by
![SE=\frac{s}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/e8h2k1oiofcrlfxgwcrd89q3iz2ire06g0.png)

In this case,
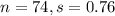
Therefore,
![SE=\frac{0.76}{\sqrt[]{74}}\approx0.0883](https://img.qammunity.org/2023/formulas/mathematics/college/fhm00hhd75f455d0x8wizdloal8zw1zadk.png)
Step 2: Find the alpha level (α)
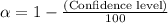

Step 3: Find the critical probability (P*)
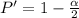
Therefore,
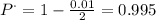
Step 4: Find the critical value (CV)
The critical value the z-score having a cumulative probability equal to the critical probability (P*).
Using the cumulative z-score table we will find the z-score with value of 0.995
Hence,
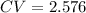
Step 5: Find the margin of error (ME)
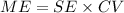
Therefore,
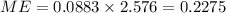
Step 6: Find the confidence interval (CI)
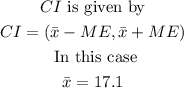
Therefore,

Hence there is a 99% probability that the true mean will lie in the confidence interval
(16.8725, 17.3275)