Given:
A card is randomly drawn from a regular deck of cards and then replaced. A second card is then drawn.
Required:
Find the probability that the first card is a spade and the second one is the jack of clubs.
Step-by-step explanation:
The total number of cards in the deck = 52
Total number of spade cards = 13
The total number of jack cards = 13
The number of jack club card = 1
The probability of an event is given by the formula:
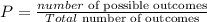
The probability that the first card is a spade is:

A second card is drawn when the first card is replaced.
The probability that the second one is the jack of clubs:

The probability that the first card is a spade and the second one is the jack of clubs:
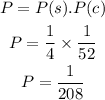
Final Answer:
Option a is the correct answer.F