Question

An ur contains 8 green balls and 7 orange balls. If Tim chooses 8 balls at random from the urn, what is the probability that he will select 3 green balls and 5orange balls? Round your to 3 decimal places.

Answer 1

Given that we have 8 green balls and 7 orange balls, making a total of 15 balls. We can select 8 balls at random from the urn containing 15 balls in

`C^n_r\text{ number of ways}`

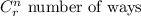
Where

`C^n_r=(n!)/((n-r)!r!)`

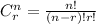
n is the total outcome

r is the desired outcome

Thus, We can select 8 balls at random from the urn containing 15 balls in

`C^(15)_8=(15!)/((15-8)!*8!)=(15!)/(7!*8!)=(15*14*13*12*11*10*9*8!)/(8!*7*6*5*4*3*2*1)=6435\text{ ways}`

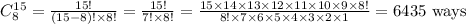
We can select 3 green balls from 8 green balls (contained in the urn) at random in

`C^8_3=(8!)/((8-3)!*3!)=(8!)/(5!*3!)=(8*7*6*5!)/(5!*3*2*1)=56\text{ ways}`

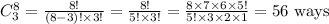
Similarly, we can select 5 orange balls from 7 orange balls (contained in the urn) at random in

`C^7_5=(7!)/((7-5)!*5!)=(7!)/(2!*5!)=(7*6*5!)/(5!*2*1)=21\text{ ways}`

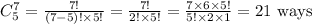
We can now calculate the probability of selecting 3 green balls and 5 orange balls as

`P(3G,5O)=P(3G)* P(5O)`

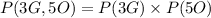
Where P(3G) is the probability of selecting 3 green balls

P(5O) is the probability of selecting 5 orange balls

`P(3G,5O)=\frac{\text{number of ways of selecting 3 green balls and 5orange balls }}{\text{number of ways of selecting 8 balls at random}}=\frac{56\text{ }*\text{ 21}}{6435}=0.1828`

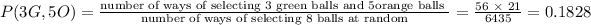
Hence, the probability of selecting 3 green balls and 5 orange balls is 0.183, in the 3 decimal places