Given that we have 8 green balls and 7 orange balls, making a total of 15 balls. We can select 8 balls at random from the urn containing 15 balls in
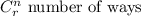
Where
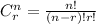
n is the total outcome
r is the desired outcome
Thus, We can select 8 balls at random from the urn containing 15 balls in

We can select 3 green balls from 8 green balls (contained in the urn) at random in
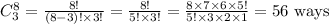
Similarly, we can select 5 orange balls from 7 orange balls (contained in the urn) at random in
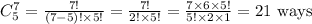
We can now calculate the probability of selecting 3 green balls and 5 orange balls as
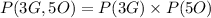
Where P(3G) is the probability of selecting 3 green balls
P(5O) is the probability of selecting 5 orange balls
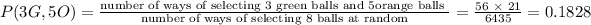
Hence, the probability of selecting 3 green balls and 5 orange balls is 0.183, in the 3 decimal places