Use the properties of the real numbers to simplify each side of each equation. Then, use the properties of equalities to solve for x.
1)
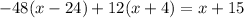
Use the distributive property to expand each parenthesis on the left hand side of the equation:
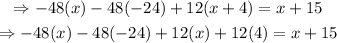
Simplify each term by multiplying the coefficients times the expressions inside the parenthesis:
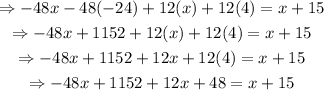
Use the commutative property to change the order of the terms on the left hand side of the equation to bring like terms together. Then, add them:
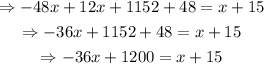
Substract x from each side of the equation:
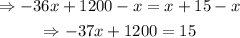
Substract 1200 from each side of the equation:
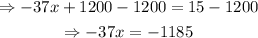
Divide both sides by -37:
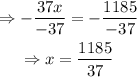
Since 1185/37 is a rational number, then this equation has a rational solution.
2)
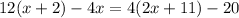
Use the distributive property to expand the parenthesis on each side of the equation, and simplify the resulting expressions:
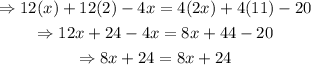
Since the expression 8x+24=8x+24 is an identity (the coefficients and constant terms are the same on both sides), then any number is a solution for this equation on the variable x.
Therefore, this equations has infinitely many solutions.