Question

Solve for X. Write down what type of solution the equation has.1) -48 (X-24) + 12 (X + 4) = X + 15 2) 12 (X + 2) - 4x = 4 (2X + 11 ) -20

Answer 1

Use the properties of the real numbers to simplify each side of each equation. Then, use the properties of equalities to solve for x.

1)

`-48(x-24)+12(x+4)=x+15`

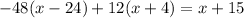
Use the distributive property to expand each parenthesis on the left hand side of the equation:

`\begin{gathered} \Rightarrow-48(x)-48(-24)+12(x+4)=x+15 \\ \Rightarrow-48(x)-48(-24)+12(x)+12(4)=x+15 \end{gathered}`

Simplify each term by multiplying the coefficients times the expressions inside the parenthesis:

`\begin{gathered} \Rightarrow-48x-48(-24)+12(x)+12(4)=x+15 \\ \Rightarrow-48x+1152+12(x)+12(4)=x+15 \\ \Rightarrow-48x+1152+12x+12(4)=x+15 \\ \Rightarrow-48x+1152+12x+48=x+15 \end{gathered}`

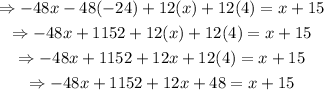
Use the commutative property to change the order of the terms on the left hand side of the equation to bring like terms together. Then, add them:

`\begin{gathered} \Rightarrow-48x+12x+1152+48=x+15 \\ \Rightarrow-36x+1152+48=x+15 \\ \Rightarrow-36x+1200=x+15 \end{gathered}`

Substract x from each side of the equation:

`\begin{gathered} \Rightarrow-36x+1200-x=x+15-x \\ \Rightarrow-37x+1200=15 \end{gathered}`

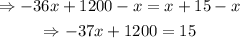
Substract 1200 from each side of the equation:

`\begin{gathered} \Rightarrow-37x+1200-1200=15-1200 \\ \Rightarrow-37x=-1185 \end{gathered}`

Divide both sides by -37:

`\begin{gathered} \Rightarrow-(37x)/(-37)=-(1185)/(-37) \\ \Rightarrow x=(1185)/(37) \end{gathered}`

Since 1185/37 is a rational number, then this equation has a rational solution.

2)

`12(x+2)-4x=4(2x+11)-20`

Use the distributive property to expand the parenthesis on each side of the equation, and simplify the resulting expressions:

`\begin{gathered} \Rightarrow12(x)+12(2)-4x=4(2x)+4(11)-20 \\ \Rightarrow12x+24-4x=8x+44-20 \\ \Rightarrow8x+24=8x+24 \end{gathered}`

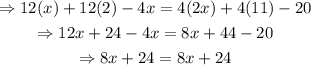
Since the expression 8x+24=8x+24 is an identity (the coefficients and constant terms are the same on both sides), then any number is a solution for this equation on the variable x.

Therefore, this equations has infinitely many solutions.