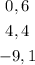Question

Find all real zeros (if any) and state the multiplicity of each

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given function

`f(x)=x^6(x-4)^4(x+9)`

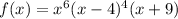
STEP 2: Define zeroes of a function

The zeros of a function are the values of x when f(x) is equal to 0. Find x such that f(x)=0

For the given function, the zeroes can be gotten as:

`\begin{gathered} x=0 \\ (x-4)=0,x-4=0,x=0+4,x=4 \\ (x+9)=0,x+9=0,x=0-9,x=-9 \end{gathered}`

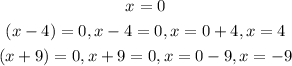
STEP 3: Get the multiciplicity

The multiplicity of each zero is the number of times that its corresponding factor appears. In other words, the multiplicities are the powers.

`\begin{gathered} x^6\Rightarrow\text{ multiciplicity is 6} \\ (x-4)^4\Rightarrow\text{multiciplicity is }4 \\ (x+9)\Rightarrow\text{multiciplicity is }1 \end{gathered}`

Hence, the real zeroes and the multiciplicity of the function are:

`\begin{gathered} 0,6 \\ 4,4 \\ -9,1 \end{gathered}`