We know that, in this case, the sample mean will be equal to the population mean, so
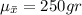
The standard deviation of the sample follows the following formula
![\sigma_{\bar{x}}=\frac{\sigma}{\sqrt[]{n}}=\frac{42gr}{\sqrt[]{20}}\approx9.4](https://img.qammunity.org/2023/formulas/mathematics/college/wx3seywqf31w8q9p1gzpq92vzq9ckocj5a.png)
The sample standard deviation is 9.4, approximately.
At last, to find the probability of the sample, first, we have to find the z-score using the following equation
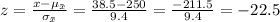
The probability value assigned to z = -22.5 is near to 0, which means that it is almost sure that there's no sample mean less than 38.5 grams.
Hence, the probability is around 0.0001.