Consider the equation,
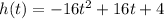
When the dough reaches the maximum height, the speed of the dough must become zero. Also we know that the velocity or speed is given by the first derivative of height,
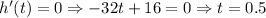
Thus, the dough reaches its maximum height at time 0.5 seconds.
Solve for the height at instant of 0.5 seconds,
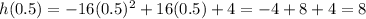
Thus, the maximum height travelled by the dough is 8 feet.
Therefore, option (D) is the correct choice.