Question

Express the integrand as a sum of partial fractions and evaluate the. Integral

Answer 1

The integral expression given is,

`\int (x+3)/(x^2+5x-6)dx`

Neglecting the integral sign, and solve the the polynomial as a partial fraction

`(x+3)/(x^2+5x-6)`

Let us factorize the denominator

`\begin{gathered} x^2+5x-6 \\ (x^2-x)+(6x-6) \\ ^{}x(x-1)+6(x-1) \\ (x+6)(x-1) \end{gathered}`

Therefore,

`(x+3)/(x^2+5x-6)=(x+3)/((x+6)(x-1))`

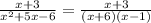
Expanding the expression using partial fraction

`\begin{gathered} (x+3)/((x+6)(x-1))=(A)/(x+6)+(B)/(x-1) \\ (x+3)/((x+6)(x-1))=(A(x-1)+B(x+6))/((x+6)(x-1)) \end{gathered}`

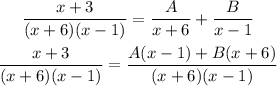
Multiply both sides by sides by (x+6)(x-1), we will have

`x+3=A(x-1)+B(x+6)`

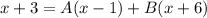
Substiute x = 1, into the equation above and solve for the value of B

`\begin{gathered} 1+3=A(1-1)+B(1+6) \\ 4=A(0)+7B_{_{}} \\ 4=_{_{_{}}}0+7B \\ 4=7B \\ (4)/(7)=(7B)/(7) \\ (4)/(7)=B \\ \Rightarrow B=(4)/(7) \end{gathered}`

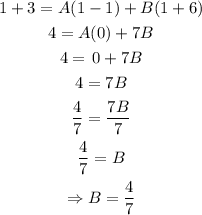
Substiute x = -6, into the equation above and solve for the value of A

`\begin{gathered} -6+3=A(-6-1)_{}+B(-6+6) \\ -3=A(-7)+B(0)=-7A+0 \\ -3=-7A \\ (-3)/(-7)=(-7A)/(-7) \\ (3)/(7)=A \\ \Rightarrow A=(3)/(7) \end{gathered}`

Hence,

`\begin{gathered} (x+3)/((x+6)(x-1))=(3)/(7(x+6))+(4)/(7(x-1)) \\ (x+3)/((x+6)(x-1))=(1)/(7)\lbrack(3)/((x+6))+(4)/((x-1))\rbrack \end{gathered}`

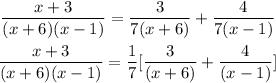
Now let us now install our answer back into the integral form

`\int (x+3)/(x^2+5x-6)dx=\int (1)/(7)\lbrack(3)/((x+6))+(4)/((x-1))\rbrack dx`

Hence, the correct option is Option C.