The integral expression given is,
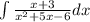
Neglecting the integral sign, and solve the the polynomial as a partial fraction
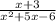
Let us factorize the denominator
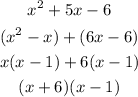
Therefore,
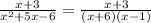
Expanding the expression using partial fraction
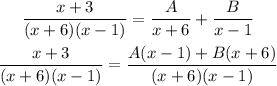
Multiply both sides by sides by (x+6)(x-1), we will have
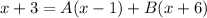
Substiute x = 1, into the equation above and solve for the value of B
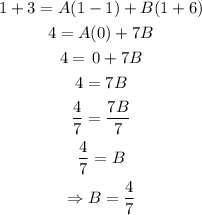
Substiute x = -6, into the equation above and solve for the value of A
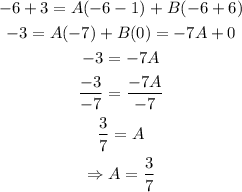
Hence,
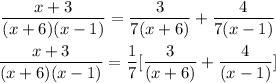
Now let us now install our answer back into the integral form
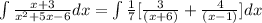
Hence, the correct option is Option C.