Given that line AD is an altitude of triangle ABC.
Equation to find the altitude AD is:
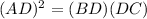
Where
BD = 3x
DC = 5x - 14
Let's solve for x:
m∠ADC = 5x + 20
m∠DAC = 2x + 2
We know that m∠ADC is 90 degrees
Thus,
5x + 20 = 90
5x = 90 - 20
5x = 70
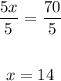
Since x = 14, we have:
BD = 3x = 3(14) = 42
DC = 5x - 14 = 5(14) - 14 = 70 - 14 = 56
Therefore

Take the square root of both sides:
![\begin{gathered} \sqrt[]{(AD)^2}=\sqrt[]{2352} \\ \\ AD\text{ = }48.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8upg9rvt0mr5tchpd60vzojmqr1lgjtz9r.png)
AD = 48.5
ANSWER:
Equation setup = (AD)² = (BD)(DC)