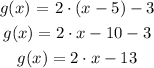Question

Let g(x) be the indicated transformation of f(x). Write the rule for g(x). linear function defined in the table horizontal translation right 5 units I’ll send you the picture

Answer 1

The first step to solve this problem is to determine the expression of the linear function. A linear function can be represented as below:

`f(x)\text{ = (}(y_2-y_1)/(x_2-x_1))x\text{ + b}`

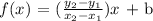
Where (x1,y1) and (x2,y2) are the coordinates of two points that belong to the function and b is a parameter that determine the "y" intercepet of the function. Applying two of the known points we can find:

`\begin{gathered} f(x)\text{ = (}(5+3)/(4))x+b \\ f(x)=(8)/(4)x+b \\ f(x)=2x+b \end{gathered}`

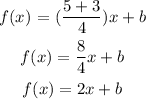
To find the value of "b" we have to apply one of the known points.

`\begin{gathered} f(0)\text{ = -3 = 2}\cdot0+b \\ -3=b \\ b=-3 \end{gathered}`

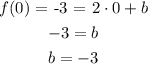
The expression is:

`f(x)=2x-3`

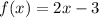
To translate a function horizontally we need to sum the distance we want to translate to the independent variable of the function, in this case "x". If the translation is to the left we need to add the positive distance and if it is to the right we need to add the negative distance.

`\begin{gathered} g(x)\text{ = 2}\cdot(x-5)-3 \\ g(x)=2\cdot x-10-3 \\ g(x)=2\cdot x-13 \end{gathered}`