We are given the following triangle:
We will determine the sides and angles of the triangle.
To determine the value o side f we will use the cosine law, which is the following:
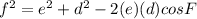
Now, we plug in the values:

Solving the operations:
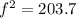
Now, we take the square root to both sides:
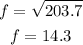
Therefore, side "f" is 14.3.
Now, we will determine angle D using the sine law:

Now, we multiply both sides by "d":
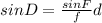
Now, we substitute the values:

Solving the operation:
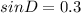
Now, w take the inverse function of the sine:
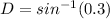
Solving the operations:
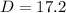
Therefore, angle D is 17.2°.
To determine angle E we will us the fact that the sum of the interiosr angles of a triangle adds p to 180:
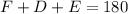
Substitting the values:
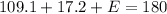
Adding the values:

Now, we subtract 126.3 from both sides:
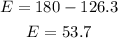
Therefre, angle E is 53.7°