Given:
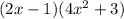
The degree of the polynomial is the highest exponent in a polynomial.
To find the degree of the polynomial, let's simplify the given expression.
We have:
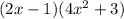
Apply distributive property:
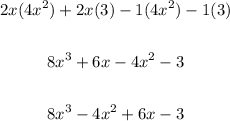
The highest exponent of the polynomial is 3.
Therefore, the polynomial is a third degree polynomial.
The leading coefficient is the coefficient of the highest exponent which is also the first term.
Therefore, the leading coefficient is 8
ANSWER:
Degree of the polynomial = 3
Leading coefficient = 8