SOLUTION:
The initial population = 75,000 in 2010
It grows at a constant rate of 2,500 per year for 5 years
If the linear function is P(t),
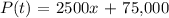
The x - intercept is;

The y - intercept is (0, 75000).
We are now to find when the population will reach 100,000.
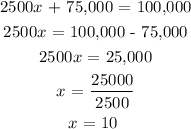
It will take the town 10 years for its population to reach 100,000, i.e in the year 2020 but we can not conclude because the g