a)
When a standing wave propagates through a string, the length of the string is a multiple of half the wavelength:
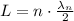
The factor n corresponds to the number of the harmonic. Then, the first harmonic is given by the condition n=1:
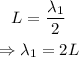
As we can see, the wavelength of the first harmonic is two times the length of the string.
Then, the wavelength of the first harmonic can be found by replacing the length L=63cm:

b)
The product of the wavelength and the frequency is the speed of the wave:
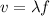
Replace λ=126cm=1.26m and f=330Hz to find the speed of the wave on the E-string:
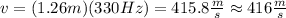
c)
The frequency of the n-th harmonic is given by:
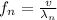
On the other hand:
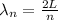
Then:

Notice that v/2L is the frequency of the first harmonic (fundamental frequency). Then:

Replace the fundamental frequency of 330Hz and n=2,3,4 to find the second, third and fourth harmonic frequencies:
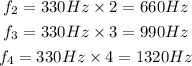
d)
Replace n=3 into the expression for the wavelength of the n-th harmonic to find the wavelength of the third harmonic:
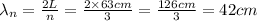
Therefore, the answers are:
a) 126cm
b) 416m/s
c) 660Hz, 990Hz, 1320Hz
d) 42cm