Question

Hello can you solve this please. (also fast because im in a rush)

Answer 1

- We can redraw the diagram as follows:

- The radius (R) of the polygon is gotten using the formula below:

`\begin{gathered} R=(s)/(2\sin(180)/(n)) \\ where, \\ n=Number\text{ of sides of the polygon} \\ s=The\text{ length of a side of the regular polygon} \end{gathered}`

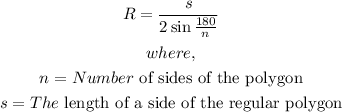
- Applying the formula, we have:

`\begin{gathered} s=4,n=5 \\ \\ R=(4)/(2\sin((180)/(5))) \\ \\ R=(2)/(\sin36)=3.4026 \end{gathered}`

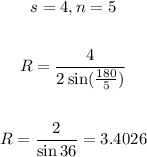
- Thus, we can use the Pythagoras theorem to find the value of the Apotem (a).

- This is done below:

`\begin{gathered} R^2=a^2+2^2 \\ a^2=R^2-2^2 \\ a^2=3.4026^2-2^2 \\ a^2=7.5778 \\ \text{ Take the square root of both sides} \\ a=√(7.5778) \\ a=2.75278...\approx2.75 \end{gathered}`

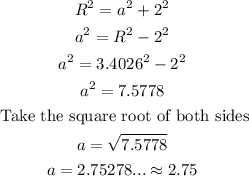
- The Apothem is 2.75

- The area is gotten below:

`\begin{gathered} A=(1)/(2)* Perimeter* Apothem \\ \\ A=(1)/(2)*20*2.75 \\ \\ A=27.5ft^2 \end{gathered}`

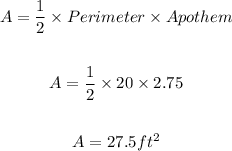
- The Area of the polygon is 27.5