Solution
- We can redraw the diagram as follows:
- The radius (R) of the polygon is gotten using the formula below:
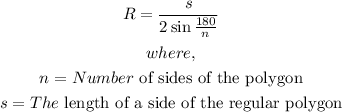
- Applying the formula, we have:
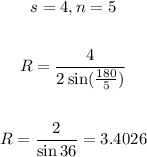
- Thus, we can use the Pythagoras theorem to find the value of the Apotem (a).
- This is done below:
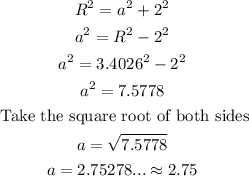
- The Apothem is 2.75
- The area is gotten below:
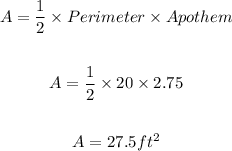
- The Area of the polygon is 27.5