Answer:
a.)

b.)
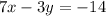
Given:
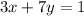
To write the given equation to its slope-intercept form, we'll just have to write it in terms of y.
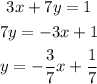
Now, perpendicular lines have the negative reciprocal of the other line.
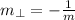
Since the slope of the given equation is -3/7,
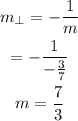
Now that we got the slope, we will substitute this to the following equation with the point (1,7)
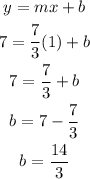
With this, we now know that the y-intercept of the equation that we are looking for is 14/3. Substituting the slope and y-intercept to the equation and we will get:
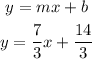
Then, to write this in its standard form,
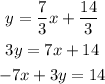
Since the first term cannot be negative, we will multiply the entire equation by -1. Therefore the answer for b is 7x - 3y = -14