we have
the system of inequalities

Remember that
If a ordered pair is a solution of the system of inequalities, then the ordered pair must satisfy both inequalities
so
we have the ordered pair
(1,2)
Verify inequality 1
x=1, y=2
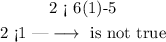
therefore
The ordered pair is not a solution of the system of inequalities
we have the ordered pair
(1,-4)
x=1, y=-4
Verify inequality 1
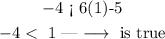
Verify inequality 2

therefore
teh ordered pair is not a solution for the system of inequalities
we have the ordered pair
(-2,6)
Verify inequality 1
x=-2, y=6

therefore
the ordered pair is not a solution of the system of inequalities
we have
(-5,10)
x=-5, y=10
Verify inequality 1

the ordered pair is not a solution of the system of inequalities