Given:
A quarterback throws a football with a velocity of 41 mph and a direction of 168°.
The wind on the field is 11 mph with a direction of 339°
So, there are 2 vectors:
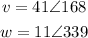
We will find the resultant speed as the sum of the vectors v and w
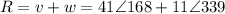
To find the sum of the vectors, convert from the polar form to the rectangular form:
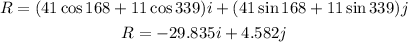
Now, we will convert from the rectangular form to the polar form to express the resultant as magnitude and angle:
![\begin{gathered} |R|=\sqrt[]{(-29.835)^2+(4.582)^2}=30.185 \\ \theta=\tan ^(-1)(4.582)/(-29.835)\approx171.268 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/c8h9s87ij7bt3by2ff4oqddkyfe2ey9dug.png)
So, the answer will be the second option: 30.185, 171°