ANSWER
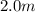
Step-by-step explanation
First, we have to find the initial length of the pendulum by applying the formula for the period:
![T=2\pi\sqrt[]{(L)/(g)}](https://img.qammunity.org/2023/formulas/physics/college/h8quhyohkhg6oj9xkblumno6z1ebdjigmr.png)
where L = length of the pendulum
g = acceleration due to gravity
Hence, we have that the initial length of the pendulum is:
![\begin{gathered} 2=2\pi\cdot\sqrt[]{(L)/(10)} \\ (2)/(2\pi)=\sqrt[]{(L)/(10)} \\ ((2)/(2\pi))^2=(L)/(10) \\ \Rightarrow L=10\cdot((2)/(2\pi))^2 \\ L=1.0m \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/x0uofplgnr0vl8kcaxwtfba9ghpex03h2d.png)
Hence, the new length of the pendulum after it is doubled is:
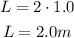
That is the answer.