ANSWER
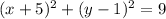
Step-by-step explanation
We want to find the equation that represents the circle given.
The general form for the equation of a circle is:

where (a, b) = center of the circle
r = radius of the circle.
From the graph, the center of the circle, K, is given as (-5, 1)
To find the radius of the circle, we have to find the distance from the center of the circle to any point on its circumference.
Let us use (-2, 1)
The formula for distance between two points is given as:
![D=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/ak1qelegvclwyfd7a2zhaqxzfglhsosdsg.png)
Therefore, the radius is:
![\begin{gathered} r=\sqrt[]{(-2-(-5))^2+(1-1)^2}=\sqrt[]{(-2+5)^2+(1-1)^2} \\ r=\sqrt[]{3^2+0^2}=\sqrt[]{3^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hmrhvqmtohn404kf9vlgeax4do2vovvfaf.png)
From there, we can find the square of both sides of the equation to find r²:
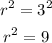
Therefore, the equation of the circle in the given graph is:
