Question

8. Calculate the area of rectangle A, the area of rectangle B,and the area of the largest rectangle.х2xDBThen, using a fraction, compare the area of rectangle A withthe area of the largest rectangle. In other words, the area ofrectangle A is what fraction of the area of the largestrectangle? Express this fraction in lowest terms.2x

Answer 1

We will solve this problem thus:

The Area of rectangle A is:

`\begin{gathered} \text{Area of A} \\ =2x*2x \\ =4x^2 \end{gathered}`

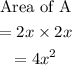
The Area of rectangle B is:

`\begin{gathered} =2x* x \\ =2x^2 \end{gathered}`

The area of the largest rectangle is:

`\begin{gathered} =2x*(2x+x) \\ =2x*(3x) \\ =6x^2 \end{gathered}`

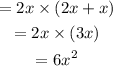
To find the fraction of rectangle A in relation to the largest rectangle, we will proceed thus:

`\begin{gathered} =\frac{\text{Area of rectangle A}}{Area\text{ of largest rectangle}} \\ =(4x^2)/(6x^2) \\ =(4)/(6) \\ =(2)/(3) \end{gathered}`

So we can say that the area of rectangle A is 2/3 times the area of the largest rectangle.