Answer
Exlplanations:
The given graph is a straight line graph where:
• y represents the ,water in gallons
,
• x represents the ,time
a) Using the coordinate points (0, 10080) and (6, 760).
Determine the slope
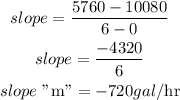
Since the line touches the y-axis at (0, 10080), hence the y-intercept "b" is 10,080
Determine the required function that model the situation
y = mx + b
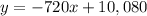
b) The rate of change is also known as the slope of the line. The rate of change is given as;
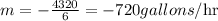
This shows that the water is draining at the rate of 720gallons per hour
c) The x-intercept is the point where the gallons of water drained "y"is zero. Substitute y = 0 into the modeled function
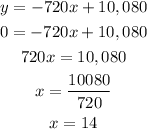
Hence the x-intercept of the function is (14, 0). This shows that the pool will be fully drained after 14 hours.
d) The y-intercept as calculated in (a) above is (0, 10080) showing that the initial gallons of water in the pool is 10,080 gallons
e) The interval where the function is positive starts from the y-intercept of the line up to the x-intercept. [14, ∞)
f) The interval where the function is negative is (-∞, 14]