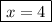Question

Show work please
\sqrt(x+12)-\sqrt(2x+1)=1

Answer 1

`x=4`

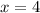
Explanation:

Given
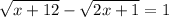`\displaystyle\\√(x+12)-√(2x+1)=1`, start by squaring both sides to work towards isolating
`x`:

`\displaystyle\\\left(√(x+12)-√(2x+1)\right)^2=\left(1\right)^2`

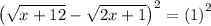
Recall
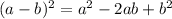`(a-b)^2=a^2-2ab+b^2` and
`√(a)\cdot √(b)=√(a\cdot b)`:

`\displaystyle\\\left(√(x+12)-√(2x+1)\right)^2=\left(1\right)^2\\\implies x+12-2√((x+12)(2x+1))+2x+1=1`

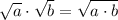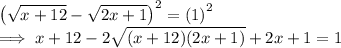
Isolate the radical:

`\displaystyle\\x+12-2√((x+12)(2x+1))+2x+1=1\\\implies -2√((x+12)(2x+1))=-3x-12\\\implies √((x+12)(2x+1))=(-3x-12)/(-2)`

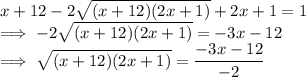
Square both sides:

`\displaystyle\\(x+12)(2x+1)=\left((-3x-12)/(-2)\right)^2`

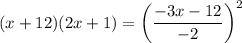
Expand using FOIL and
`(a+b)^2=a^2+2ab+b^2`:

`\displaystyle\\2x^2+25x+12=(9)/(4)x^2+18x+36`

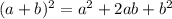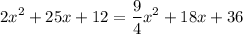
Move everything to one side to get a quadratic:

`\displaystyle-(1)/(4)x^2+7x-24=0`

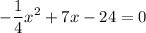
Solving using the quadratic formula:

A quadratic in
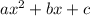`ax^2+bx+c` has real solutions
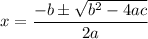`\displaystyle x=(-b\pm √(b^2-4ac))/(2a)`. In
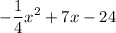`\displaystyle-(1)/(4)x^2+7x-24`, assign values:

`\displaystyle \\a=-(1)/(4)\\b=7\\c=-24`

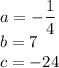
Solving yields:

`\displaystyle\\x=\frac{-7\pm \sqrt{7^2-4\left(-(1)/(4)\right)\left(-24\right)}}{2\left(-(1)/(4)\right)}\\\\x=(-7\pm √(25))/(-(1)/(2))\\\\\begin{cases}x=(-7+5)/(-0.5)=(-2)/(-0.5)=\boxed{4}\\x=(-7-5)/(-0.5)=(-12)/(-0.5)=24 \:(\text{Extraneous})\end{cases}`

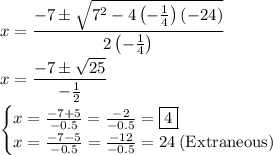
Only
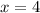`x=4` works when plugged in the original equation. Therefore,
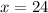`x=24` is extraneous and the only solution is
`\boxed{x=4}`