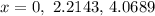Given:
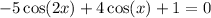
Let's solve the equation over the interval:
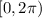
To find the equation over the interval, apply the double angle identity:
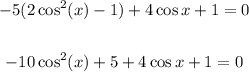
Combine like terms:
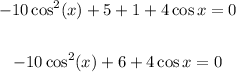
Factor:
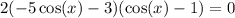
Set the individual factors to zero and solve:
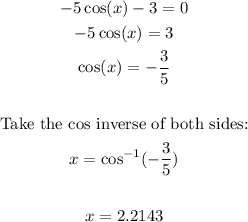
Also, the cosine function is negative in the second and third quadrants.
Subtract the reference angle from 2π to find the other angle:
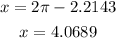
Set the second factor to zero anmd solve for x:
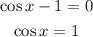
Take the inverse cosine of both sides:
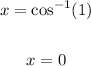
The cosine function is positive in quandrant I and IV, to find the other angle, subtract the reference angle from 2π.
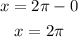
Let's find the period of the function:
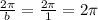
Since the period is 2π, values will repeat every 2π radians in all direction.
Here, we have the interval: [0, 2π).
This means 2π is not an included solution.
Therefore, the solutions to the given equation over the interval are:
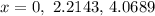
ANSWER: