ANSWER
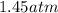
Step-by-step explanation
Parameters given:
Speed of water at point 1, v1 = 5.1 m/s
Diameter of pipe at point 1, d1 = 3.5 cm = 0.035 m
Pressure, P1 = 1.9 atm
Diameter of pipe at point 2, d2 = 2.4 cm = 0.024 m
Atmospheric pressure = 1.013 * 10^5 Pa
Density of water = 1000 kg/m^3
First, we have to find the speed of the water at the smaller end of the pipe. To do this, apply the Bernoulli continuity equation:
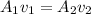
where A1 and A2 are the cross-sectional areas of the pipes at point 1 and point2 respectively.
Substituting the given values into the equation above:
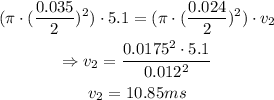
Now, we have to apply Bernoulli's equation to find the pressure at the constricted segment:
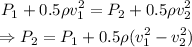
Substitute the known values into the equation and solve for P2, we have:
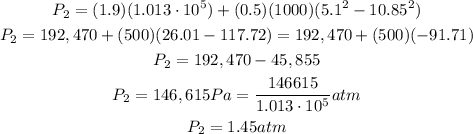
That is the answer.