Question

A rectangle has an area of 208 square inches. The width is 2 more than 3 times the length. Find the length and width, in inches, of the rectangle.

Answer 1

Step-by-step explanation:

Given;

We are given the following information. A rectangle has an area of 208 square inches. The width is 2 more than 3 times the length.

Required;

We are required to find the length and the width.

Step-by-step solution;

If the length is given as l, then the width would be 2 plus 3 times l. That is;

`\begin{gathered} If\text{ } \\ length=l \\ Then \\ width=2+3l \end{gathered}`

Note also that the area of a rectangle is calculated as;

`Area=l* w`

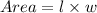
Given that the area is 208 square inches, we can set up the following information;

`\begin{gathered} Area=l* w \\ Therefore: \\ 208=l(2+3l) \end{gathered}`

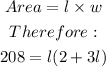
We simplify the parenthesis;

`208=2l+3l^2`

We can move all terms to one side of the equation and we have;

`3l^2+2l-208=0`

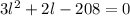
Now we have a quadratic equation and we shall solve this by the quadratic equation formula.

`x=(-b\pm√(b^2-4ac))/(2a)`

The variables in this case are;

`a=3,b=2,c=-208`

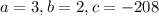
We can now substitute these into the quadratic formula and solve as follows;

`x=(-2\pm√(2^2-4(3)(-208)))/(2(3))`
`x=(-2\pm√(4+2496))/(6)`
`x=(-2\pm√(2500))/(6)`
`x=(-2\pm50)/(6)`

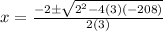
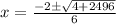
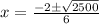
We can now evaluate separately as follows;

`\begin{gathered} x_1=(-2+50)/(6)=(48)/(6)=8 \\ Also: \\ x_2=(-2-50)/(6)=(-52)/(6)=-(26)/(3) \end{gathered}`

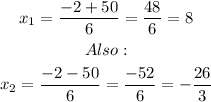
Therefore, the two values of l will be,

`\begin{gathered} l_1=8in \\ l_2=-(26)/(3)in \end{gathered}`

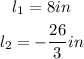
We shall take the positive value only, since we know that the length or width of any plane shape is always a positive value.

Therefore, the length of the rectangle is 8 inches. The width can now be determined as follows;

`w=2+3l`
`w=2+3(8)`
`w=2+24=26`

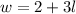
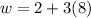
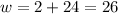
Therefore;

ANSWER:

`\begin{gathered} length=8in \\ width=26in \end{gathered}`