Question

A bar of mass M and length L = 4 meters is pivoted on a fulcrum that is d = 1.8 meters away from the left end. Attached to the left end, a mass m = 5 kg hangs at rest and keeps the system in equilibrium. What is the mass of the bar?

Answer 1

The given problem can be exemplified in the following diagram:

The weight of the bar is concentrated in its center of mass which is located in the middle of the longitude of the bar. We can add the total torques at the point where the pivot touches the bar and we get:

Here we have used momentum counter-clockwise as positive. Since the system is in equilibrium the sum of the torques must be equal to zero:

Now we solve the operations, we will use for the acceleration of gravity 9.8 meters per second squared:

`88.2Nm-1.96M=0`

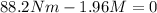
Now we solve for the mass "M" first by subtracting 88.2Nm from both sides:

`-1.96M=-88.2Nm`

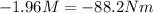
Now we divide both sides by -1.96:

`M=(-88.2Nm)/(1.96m(m)/(s^2))`

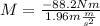
Solving the operations we get:

Therefore, the mass of the bar is 45 kg.