Question

Write a polynomial function of least degree with real coefficients in standard form that has the given zeros.–2, –4, –3 + 4i x2 + 6x + 8x4 + 12x3 + 198x + 200x4 + 12x3 + 69x2 + 198x + 200x4 + 69x2 + 198x + 200

Answer 1

Write the polynomial function of least degree with real coefficients in standard form:

According to the complex conjugate root theorem, if a complex number a+ib is a zero of a polynomial, then its conjugate a-ib is also a zero of than polynomial.

–3 + 4i is zero of the polynomial. So, by complex conjugate root theorem -3-4i is also a zero of required polynomial.

If c is a zero of p(x), then (x-c) is a factor of p(x).

–2, –4, –3 + 4i, -3-4i are zeroes of the polynomials. So, (x+2), (x+4), (x+3-4i), (x+3+4i) are the factors of the required polynomial.

Let the required polynomial be p(x), so

`\begin{gathered} p(x)=(x+2)(x+4)(x-3+4i^2)(x+3+4i^2)_{} \\ P(x)=(x^2+2x+4x+8)(x+3)^2-(4i^2)^2) \\ (a^2-b^2)=(a-b)(a+b) \\ p(x)=x^2+6x+8)(x^2+6x+9-16i^2 \\ i^2\text{=-1} \\ p(x)=(x^2+6x+8)(x^2+6x+9-16(-1) \\ p(x)=(x^2+6x+8)(x^2+6x+9+16^{} \\ p(x)=(x^2+6x+8)(x^2+6x+25) \end{gathered}`

`\begin{gathered} p(x)=(x^2+6x+8)(x^2+6x+25) \\ p(x)=x^2(x^2+6x+8)+6(x^2+6x+8)+25(x^2+6x+8) \\ p(x)=x^4+12x^3+69x^2+198x+200 \end{gathered}`

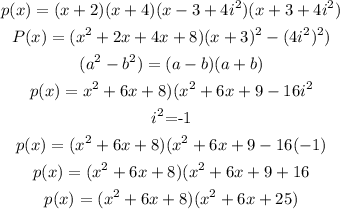
Combining like terms, we get

Therefore, the required polynomial is x^2 + 12x^3 +69x^2 + 198x + 200

Hence the correct answer is Option C