Write the polynomial function of least degree with real coefficients in standard form:
According to the complex conjugate root theorem, if a complex number a+ib is a zero of a polynomial, then its conjugate a-ib is also a zero of than polynomial.
–3 + 4i is zero of the polynomial. So, by complex conjugate root theorem -3-4i is also a zero of required polynomial.
If c is a zero of p(x), then (x-c) is a factor of p(x).
–2, –4, –3 + 4i, -3-4i are zeroes of the polynomials. So, (x+2), (x+4), (x+3-4i), (x+3+4i) are the factors of the required polynomial.
Let the required polynomial be p(x), so
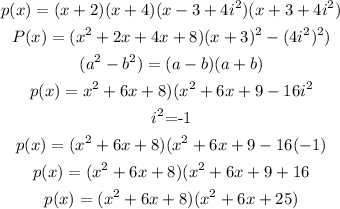
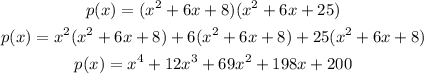
Combining like terms, we get
Therefore, the required polynomial is x^2 + 12x^3 +69x^2 + 198x + 200
Hence the correct answer is Option C