Question

A population of beetles are growing according to a linear growth model. The initial population (week 0) is P0=3, and the population after 8 weeks is P8=51Find an explicit formula for the beetle population after n weeks.Pn =After how many weeks will the beetle population reach 165?

Answer 1

Since the population grows following a linear model, this means that we can write the relationship between the population and the time in a linear equation.

The standard form of a linear equation is:

`y=mx+b`

Where:

m = slope

b = y-intercept

Also, given two points, P and Q, we can find the slope of the line that connects them by:

`\begin{gathered} \begin{cases}P={(x_P},y_P) \\ Q={(x_Q},y_Q)\end{cases} \\ . \\ m=(y_Q-y_P)/(x_Q-x_P) \end{gathered}`

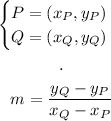
The problem tells us that at week 0, the population is 3, and at week 8 the population is 51. Those are two points that we can call:

P = (0, 3)

Q = (8, 51)

Now, we can calculate the slope:

`m=(51-3)/(8-0)=(48)/(8)=6`

And since the y-intercept is the value of y when x = 0, the y-intercept is the population at week 0, b = 3

Then:

`P_n=6n+3`

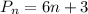
Is the explicit formula for the beetle population after n weeks.

Now, to find after how many weeks the beetle population will be 165, we substitute in the equation P = 165:

`165=6n+3`

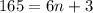
And solve:

`\begin{gathered} 165-3=6n \\ . \\ n=(162)/(6)=27 \end{gathered}`

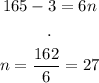
Thus, after 27 weeks the population will be 165.