ANSWER:
C = 43.61 degrees
A = 71.52 degrees
Step-by-step explanation:
Given:
To find:
The measure of angles C and A
We'll use the below the laws of cosines to determine the measure of angles C and A;
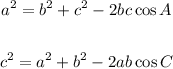
where;
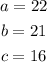
Let's go ahead and substitute the above values into the equation and solve for C;
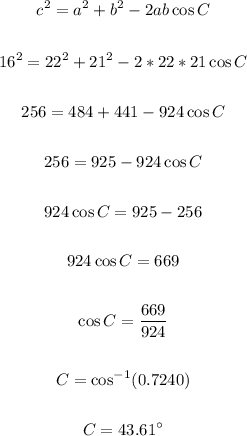
Let's go ahead and substitute the above values into the equation and solve for A;
