Question

Solve the triangle below. Use the law of cosines to find the measure of angle C.Use any method you like to find measure of angle A.

Answer 1

C = 43.61 degrees

A = 71.52 degrees

Step-by-step explanation:

Given:

To find:

The measure of angles C and A

We'll use the below the laws of cosines to determine the measure of angles C and A;

`\begin{gathered} a^2=b^2+c^2-2bc\cos A \\ \\ c^2=a^2+b^2-2ab\cos C \end{gathered}`

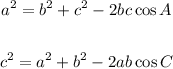
where;

`\begin{gathered} a=22 \\ b=21 \\ c=16 \end{gathered}`

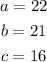
Let's go ahead and substitute the above values into the equation and solve for C;

`\begin{gathered} c^2=a^2+b^2-2ab\cos C \\ \\ 16^2=22^2+21^2-2*22*21\cos C \\ \\ 256=484+441-924\cos C \\ \\ 256=925-924\cos C \\ \\ 924\cos C=925-256 \\ \\ 924\cos C=669 \\ \\ \cos C=(669)/(924) \\ \\ C=\cos^(-1)(0.7240) \\ \\ C=43.61^(\circ) \end{gathered}`

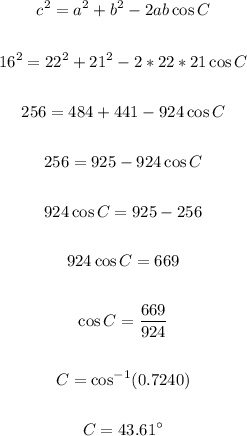
Let's go ahead and substitute the above values into the equation and solve for A;

`\begin{gathered} 22^2=21^2+16^2-2*21*16\cos A \\ \\ 484=441+256-672\cos A \\ \\ 484=697-672\cos A \\ \\ 672\cos A=697-484 \\ \\ 672\cos A=213 \\ \\ \cos A=(213)/(672) \\ \\ A=\cos^(-1)(0.31696) \\ \\ A=71.52^(\circ) \end{gathered}`