Given the equation:

If we re-arrange the equation
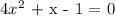
To determine the number of solutions,
Step 1: compare with the equation
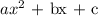
So that a = 4
b = 1
c = -1
Step 2: Substitute the values of a, b, and c into the discriminant
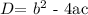
Where D is the discriminant
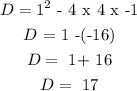
Since the discriminant, D, is greater than 1, It has two real roots.
Hence, the number of solutions is Two different real solutions
For the second part of the question
![x\text{ = }\frac{-b\text{ }\pm\sqrt[]{b^2\text{ -4ac}}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/qh5abmhx8ejwnqxnky4a0st3j9bkzvp5kh.png)
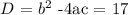
![x\text{ =}\frac{-1\pm\sqrt[]{17}\text{ }}{2\text{ x 4}}](https://img.qammunity.org/2023/formulas/mathematics/college/iffbvuk4a16axob72ts0sh9qslbvt2wnzm.png)
![x\text{ =}\frac{-1\text{ }\pm\sqrt[]{17}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/zgaxeu4pchztqvdt4mcdb2372ggj3ws5lf.png)
Therefore,
![x\text{ =}\frac{-1\text{ +}\sqrt[]{17}}{8}\text{ , x =}\frac{-1\text{ -}\sqrt[]{17}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/yugmb55vrj8okwbzc6356nzz8t3lx54axs.png)