Question

4. Suppose that the water level of a river is 34 feet and that it is receding at a rate of 0.5 foot per day. a. Write a linear equation in slope-intercept form that relates the water level to the number of days. __________________________ b. After 38 days, how high is the water level of the river? c. In how many days will the water level be 26 feet?

Answer 1

Question A:

A linear equation in slope-intercept form is of the form:

From the question, we can conclude that:

m = -0.5 (the slope is negative because the water level is reducing)

c = 34.

Thus, the equation is given as:

`\begin{gathered} y=-0.5x+34 \\ \text{where,} \\ x=\text{ number of days} \\ y=\text{level of water in feet} \end{gathered}`

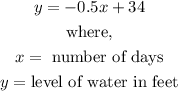
Question B:

`\begin{gathered} \text{After 38 days, we need to find the level of water.} \\ \text{This means that:} \\ x=38\text{ and we need to find the value of }y \\ \\ y=-0.5(38)+34 \\ y=-19+34 \\ \therefore y=15\text{feet} \end{gathered}`

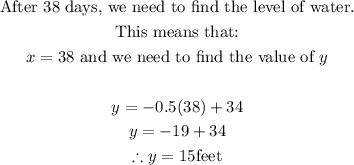
Thus, the water level after 38 days is 15 feet

Question C:

`\begin{gathered} \text{ We need the number of days when the water level is 26 feet.} \\ \text{This means that:} \\ y=26,x=? \\ \\ \text{Thus, we can say:} \\ 26=-0.5x+34 \\ \text{Subtract 34 from both sides} \\ 26-34=-0.5x \\ -8=-0.5x \\ \text{Divide both sides by }-0.5 \\ -(0.5x)/(-0.5)=-(8)/(-0.5) \\ \\ x=16 \end{gathered}`

16 days have elapsed when the water level is at 26 feet

Answer

Question A:

The equation is:

`y=-0.5x+34`

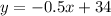
Question B:

The water level after 38 days is 15 feet

Question C:

16 days have elapsed when the water level is at 26 feet