Question A:
A linear equation in slope-intercept form is of the form:
![\begin{gathered} y=mx+c \\ \text{where,} \\ m=\text{slope of the linear graph} \\ c=y-\text{intercept of the linear graph.} \\ \\ \\ \text{For our question, }y\text{ represents the water level of the river in feet. }x\text{ represents the number of days, }m\text{ represents} \\ \text{the rate of change of the level of water per day, while }c\text{ is the initial level of water.} \end{gathered}]()
From the question, we can conclude that:
m = -0.5 (the slope is negative because the water level is reducing)
c = 34.
Thus, the equation is given as:
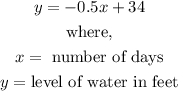
Question B:
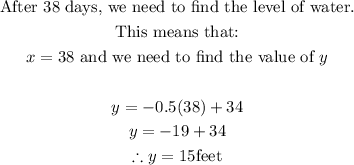
Thus, the water level after 38 days is 15 feet
Question C:

16 days have elapsed when the water level is at 26 feet
Answer
Question A:
The equation is:
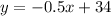
Question B:
The water level after 38 days is 15 feet
Question C:
16 days have elapsed when the water level is at 26 feet