Question

The length of the longer leg of a right triangle is 3 cm more than three times the length of the shorter leg. The length of the hypotenuse is 4 cm more than three times the length of the shorter leg. Find the side lengths of the triangle.

Answer 1

Let l be the length of the longer leg, w be the length of the shorter leg and h be the length of the hypotenuse.

It is given that the length of the the longer leg of a right triangle is 3 cm more than three times the length of the shorter leg.

Hence, we can write

`l=3+3w\text{ ----(1)}`

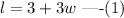
It is given that the length of the hypotenuse is 4 cm more than three times the length of the shorter leg. Hence, we can write

`h=4+3w\text{ ----(2)}`

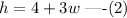
Applying Pythagoras theorem to the right triangle,

`\begin{gathered} \text{Hypotenuse}^2=Leg^2_1+Leg^2_2 \\ h^2=l^2+w^2 \end{gathered}`

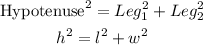
Replace equation (1) for l and equation (2) for w in the above equation.

`\begin{gathered} (4+3w)^2=(3+3w)^2+w^2 \\ 4^2+2*4*3w+(3w)^2=3^2+2*3*3w+(3w)^2+w^2 \\ 16+24w+9w^2=9+18w+9w^2+w^2 \\ 0=9-16+18w-24w+w^2 \\ 0=-7-6w+w^2 \\ w^2-6w-7=0 \end{gathered}`

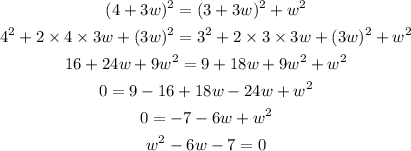
Solving further,

`\begin{gathered} (w-7)(w+1)=0 \\ (w-7)=0\text{ or (w+1)=0} \\ w=7\text{ or w=-1} \end{gathered}`

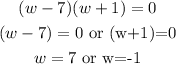
Since width cannot be negative, w=7.

Now, the length of the longer leg is,

`\begin{gathered} l=3+3w \\ =3+3*7 \\ =3+21 \\ =24 \end{gathered}`

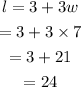
The length of the hypotenuse is,

`\begin{gathered} h=4+3w \\ =4+3*7 \\ =4+21 \\ =25 \end{gathered}`

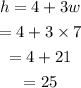
Therefore, the length of the shorter leg is 7 cm.

The length of the longer leg is 24cm.

The length of the hypotenuse is 25 cm.