Let l be the length of the longer leg, w be the length of the shorter leg and h be the length of the hypotenuse.
It is given that the length of the the longer leg of a right triangle is 3 cm more than three times the length of the shorter leg.
Hence, we can write
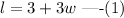
It is given that the length of the hypotenuse is 4 cm more than three times the length of the shorter leg. Hence, we can write
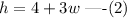
Applying Pythagoras theorem to the right triangle,
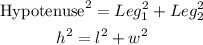
Replace equation (1) for l and equation (2) for w in the above equation.
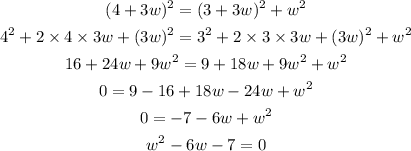
Solving further,
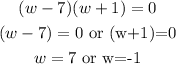
Since width cannot be negative, w=7.
Now, the length of the longer leg is,
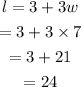
The length of the hypotenuse is,
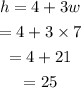
Therefore, the length of the shorter leg is 7 cm.
The length of the longer leg is 24cm.
The length of the hypotenuse is 25 cm.