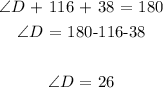Here, we want to calculate the measure of angle D
Firstly, we can calculate the measure of angle A
Since BE and AD are perpendicular, it follws that triangle ABE is a right angled triangle
Thus,
52 + A = 90
A = 90-52
A = 38
Now, from the question, we are told that EBD and CBD are congruent, meaning that they are equal
We can deduce from the diagarm that;
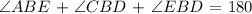
The reason for this is that they are all on a straight line and the measure of angles on a straight line is 180
Thus, since we have the two angles equal, then;
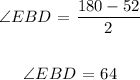
The measure of angle B in triangle ABD would be 64 + 52 = 116.
Since we have two angles out of triangle ABD, we can get the measure of the third angle which is angle D (Sum of angles in a triangle = 180)
Mathematically, that would be;