Question

State the domain of the function g(x)=3- √x

Answer 1

We are asked to find the Domain of the function:

`g(x)=3-\sqrt[]{x}`

So we need to find what are the x-values that can give us valid answers for the function g(x). We notice that the variable x is inside the square root, so for the square root to produce a real number value, the "radicand" (expression inside the root) must be a number larger than or equal zero, otherwise the answer would not be a real number.

So here we find that our Domain must be restricted to x-values larger than or equal to zero.

This in set builder notation is written as:

`\text{Domain}=\mleft\lbrace x\mright|x\ge0\}`

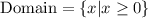
That reads: All x-values such that x is larger than or equal to zero:

Domain = x